Les catégories

La théorie des catégories, créée dans les années 1940, a progressivement remplacé la théorie des ensembles comme outil de base pour exprimer les structures mathématiques. Dans les ensembles, on travaille avec les éléments ; dans les catégories, on travaille avec les flèches, qui expriment une relation entre 2 objets.
Le définition d'une catégorie est très simple, mais travailler avec des catégories oblige à changer notre manière habituelle de penser (utiliser les flèches au lieu des éléments). La théorie des catégories contient de nombreuses notions : construction universelle, foncteurs, transformations naturelles.

Historique

Les catégories ont été créées par deux mathématiciens américains, Saunders Mac Lane et Samuel Eilenberg. Les catégories ont intégré l'informatique théorique en 1980. On avait déjà l'isomorphisme de Curry-Howard, qui assimile un type informatique à une proposition logique - et le passage d'un type à l'autre (une fonction pure) à une démonstration. Lambek a montré qu'un type (ou une proposition logique) peut aussi être assimilé à un objet d'une "catégorie cartésienne fermée" - et les fonctions (ou preuves) aux flèches de cette catégorie. On parle de la correspondance (ou isomorphisme) de Curry-Howard-Lambek.

Définition

Dans une catégorie, on a des objets et des flèches qui vont d'un objet à l'autre. Une flèche exprime une relation entre 2 objets.

Une catégorie est donc un graphe orienté : les objets sont les sommets et les flèches sont les arêtes.
Mais pour qu'un graphe orienté mérite le nom de catégorie, les flèches doivent vérifier certaines propriétés :
  1. Identité : Tout objet doit avoir une flèche qui part de cet objet et arrive à cet objet sans rien changer.
    On note idA l'indentité de l'objet A.
  2. Composition : s'il existe une flèche de A vers B et une flèche de B vers C, alors il doit exister une flèche qui va directement de A à C.
    Aller de A à B puis de B à C revient exactement au même que d'aller directement de A à C.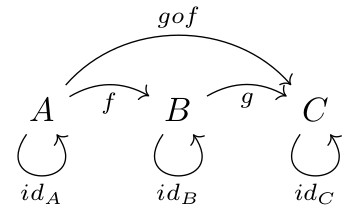 Composition dans une catégorie La flèche qui va directement de A à C s'appelle la composée de f et de g.
    On note g ( f ) = g ∘ f
    g∘f se prononce " g rond f ". Cette notation n'est pas intuitive car elle est à l'envers, mais elle est logique, car on applique g au résultat de f.
    A la place de " g rond f ", on pourrait dire " g de f ".
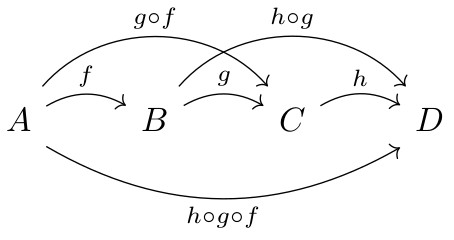
  3. Associativité : le chemin parcouru ne change pas le résultat. Associativité dans une catégorie h ∘ (g ∘ f) = (h ∘ g) ∘ f
    La flèche qui va directement de A à D peut donc s'écrire h ∘ g ∘ f, sans les parenthèses.
Et c'est tout.

Le fait d'avoir des flèches en plus des objets permet de représenter de nombreux phénomènes de manière naturelle.
Dans la théorie des ensembles, on travaille avc les éléments.
Dans la théorie des catégories, on travaille avec les flèches.
Pour une illustration de cette différence, voir les fonctions

Catégorie des ensembles

La catégorie la plus familière à étudier est la catégorie des ensembles, notée Set ou Ens, qui contient tous les ensembles possibles.
Dans cette catégorie,
- un objet est un ensemble,
- une flèche est une relation entre 2 ensembles.

Dans cette catégorie, n'importe quel ensemble est représenté par un objet. Un objet est sans structure, comme un point, on n'a pas de moyen d'utiliser les propriétés internes des objets.
On utilise à la place les propriétés des flèches et de leur composition.
Ce qui est déroutant car on connaît les ensembles avec lesquels on travaille, on est habitué à utiliser leur structure interne pour les étudier.

Catégorie des types et des fonctions

Cette catégorie permet de modéliser un langage informatique comprenant : C'est un cas particulier de la catégorie des ensembles.

Types de données

Un type de donnée peut être représenté par un ensemble dont les éléments sont les valeurs que peut prendre ce type.

Ce sont des ensembles finis ou infinis :
TypeEnsembleN : cardinal de l'ensemble
Boolean true, false 2
Char 'a', 'b', ... 128
Integer 1, 2, 3 ... ∞ infini
Real 0.0001, 0.0002 ... ∞ infini
String "", "a", "aa" ... ∞ infini
Certains types ont en théorie un nombre inifni de valeurs mais en pratique un nombre fini car limité par les capacités de la machine.

Fonctions pures

Une fonction au sens mathématique du terme : f(x) = y, prend en entrée un paramètre et renvoie une valeur.
La définition d'une fonction pure est moins stricte ; une fonction est dite pure si : Par exemple : 
// char --> boolean
boolean isVoyelle(char c){ }
En pratique, les fonctions diffèrent des fonctions mathématiques car elles peuvent : Mais toutes ces complexités peuvent être construites à partir de fonctions pures à un seul paramètre, ce qui permet de définir une catégorie des types comme un cas particulier de Set car un type peut être représenté par un ensemble.

La catégorie des types fournit donc une représentation mathématique d'un langage fonctionnel.

Foncteurs

Un foncteur transforme une catégorie en une autre.
Lorsqu'on spécifie un foncteur, il faut

Constructeur

Un foncteur couramment utilisé en informatique est le contructeur de type.

Lorsqu'on écrit en java : 
class Animal {}
cela permet de créer des objet de type Animal : 
Animal a = new Animal();
On passe bien d'une première catégorie, dont les objets sont les types manipulés par notre programme : String etc.
à une deuxième catégorie, dont les objets sont les types précédent PLUS le nouveau type, Animal.

Quelques liens