Bases 2 10 16...

De la même manière que nous utilisons des lettres pour former des mots, nous utilisons des chiffres pour former des nombres.
LettreMot
ChiffreNombre
Les chiffres et les lettres sont donc des symboles abstraits, qui ne représentent rien de particulier dans le monde réel.
Avec les chiffres, on forme des nombres, qui ont comme les mots une signification dans l'univers qu'on étudie.

Notation

"45 en base 10 = 101101 en base 2" se note :
(45)10 = (101101)2

Base 10 - Système décimal

Nous sommes habitués à compter en base 10, c'est à dire que nous utilisons 10 chiffres différents pour former des nombres : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Lorsqu'on forme un nombre, on utilise les puissances successives de 10.
2 652 = 2 x 1000 + 6 x 100 + 5 x 10 + 2
= 2 x 103 + 6 x 102 + 5 x 101 + 2 x 100
(2 652)10 = (2 652)10
104
10 000		 103
1 000		 102
100		 101
10		 100
1		 SOMME
base 10
2 6 5 2
2 000 + 600 + 50 + 2 = 2 652
De la même manière, on peut exprimer des nombres dans différentes bases.

Base 7

Si on comptait en base 7, on ne disposerait que de 7 chiffres : 0, 1, 2, 3, 4, 5, 6.

Le nombre 2 652 écrit en base 7 ne représente pas la même quantité que 2 652 écrit en base 10 :
74
2 401		 73
343		 72
49		 71
7		 70
1		 SOMME
base 7
2 6 5 2
2 x 343 6 x 49 5 x 7 2 x 1
646 + 294 + 35 + 2 = 977
(2 652)7 = (977)10

Base 2 - Système binaire

En base 2, nous n'utilisons que 2 chiffres : 0 et 1.
Le principe pour écrire un nombre est le même qu'en base 10.
Par exemple,
101101 = 1 x 25 + 0 x 24 + 1 x 23 + 1 x 22 + 0 x 21 + 1 x 20
= 32 + 8 + 4 + 1
= 45
(101101)2 = (45)10
210
1024		 29
512		 28
256		 27
128		 26
64		 25
32		 24
16		 23
8		 22
4		 21
2		 20
1		 SOMME
1
32		 0
0		 1
8		 1
4		 0
0		 1
1
45

Conversion base 2 → base 10

On utilise simplement la définition précédente pour faire le calcul.
Exercices
Convertir en base 10 les nombres suivants exprimés en base 2 :
  • 0
  • 1
  • 10
  • 111
  • 1000
  • 100110
  • 1010110110

Conversion base 10 → base 2
Méthode des restes

Par exemple, si on veut convertir le nombre 45 en base 2 :
On se demande : quelle est la plus grande puissance de 2 qui "tient" dans 45 ?
La réponse est 32 (25).
Nous indique qu'il y a un 1 dans le 6ème bit :
25
32		 24
16		 23
8		 22
4		 21
2		 20
1		 SOMME
1
32		 ?
?		 ?
?		 ?
?		 ?
?		 ?
?
45
On a casé 32, reste à caser 45 - 32 = 13

On recommence avec 13 : quelle est la plus grande puissance de 2 qui "tient" dans 13 ?
La réponse est 8 = 23
25
32		 24
16		 23
8		 22
4		 21
2		 20
1		 SOMME
1
32		 0
0		 1
8		 ?
?		 ?
?		 ?
?
45
Reste à caser 13 - 8 = 5

On recommence avec 5 : quelle est la plus grande puissance de 2 qui "tient" dans 5 ?
La réponse est 4 = 22
25
32		 24
16		 23
8		 22
4		 21
2		 20
1		 SOMME
1
32		 0
0		 1
8		 1
1		 ?
?		 ?
?
45
Reste à caser 5 - 4 = 1

On recommence avec 1 : quelle est la plus grande puissance de 2 qui "tient" dans 1 ?
La réponse est 1 = 20
25
32		 24
16		 23
8		 22
4		 21
2		 20
1		 SOMME
1
32		 0
0		 1
8		 1
4		 0
0		 1
1
45

Reste à caser 1 - 1 = 0

Lorsque le reste vaut 0, le processus est terminé.

Finalement, 45 = 25 + 23 + 22 + 20
Ecrire en base 2 les nombres suivants écrits en base 10.
  • 0
  • 1
  • 2
  • 3
  • 10
  • 54
  • 255
  • 256
  • 473

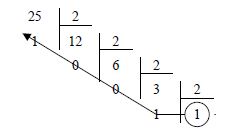
Conversion base 10 → base 2
Méthode des divisions successives

La méthode de la division successive sert à transformer n'importe quel nombre dans n'importe quelle base.
Pour transformer un nombre décimal en un nombre de base « a », il suffit de diviser le nombre décimal par la base « a » jusqu'à obtenir un quotient inférieur à la base. Le résultat recherché se compose du dernier quotient et de tous les restes des divisions successives pris dans l'ordre inverse.
Conversion par divisions successives

Addition, multiplication binaire

Fonctionne comme en base 10, mais les tables d'addition et de multiplication sont beaucoup plus simples !
Addition
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10 		Multiplication
0 x 0 = 0
0 x 1 = 0
1 x 0 = 0
1 x 1 = 1
Exemple d'addition :

    1 1      ← retenues
    1 0 1
  + 1 1 1
 ------------
  1 1 0 0

Exemple de multiplication :
       1 0 1 0
     x 1 0 1 1
 ---------------
       1 0 1 0
     1 0 1 0
   0 0 0 0
 1 0 0 0
 ---------------
 1 0 1 1 1 1 0
Effectuer les additions binaires suivantes :
  • 10 + 101
  • 111 + 101
  • 100101 + 111101
Effectuer les multiplications binaires suivantes :
  • 100 x 100
  • 10001 x 110

Remarques

Exprimer une puissance de 2

Une puissance exacte de 2 (1, 2, 4, 8...) est très facile à exprimer en base 2.
Par exemple, 64 = 26 = 64 = 1 x 26 + 0 x 25 + 0 x 24 + 0 x 23 + 0 x 22 + 0 x 21 + 0 x 20
Donc (64)10 = (1000000)2
Remarquez que la situation est identique pour toutes les bases, par exemple :

Multiplier par 2

En base 2, multiplier par 2 revient à "rajouter un 0 à droite".
Par exemple (45)10 = (101101)2
(45)10 = 1 x 25 + 0 x 24 + 1 x 23 + 1 x 22 + 0 x 21 + 1 x 20
(90)10 = 1 x 26 + 0 x 25 + 1 x 24 + 1 x 23 + 0 x 22 + 1 x 21 + 0 x 20
On a la multiplication binaire : 101101 x 10 = 1011010

On est exactement dans la même situation que lorsqu'on multiplie par 10 en base 10.

Octets

On appelle octet un nombre exprimé en binaire constitué de 8 chiffres (0 ou 1).
Ex : 1 0 1 1 0 0 1 0
On dit que un octet est un mot binaire de longueur 8 (on appelle mot binaire une suite de 0 et de 1).
La mémoire de l'ordinateur conserve toutes les données sous forme binaire. Pour stocker des caractères, on a associé à chaque caractère un code numérique : c'est le code ASCII (American Standard Code for Information Interchange - « Code Americain Standard pour l'Echange d'Informations »). Le code ASCII d'origine représentait les caractères sur 7 bits (c'est-à-dire 128 caractères possibles, de 0 à 127).
Pour les lettres majuscules, on a : A: 65, B: 66 ... Z: 90
Pour les lettres minuscules, on a : a: 97, b: 98 ... z: 122
En utilisant le code ASCII, représentez comment le mot SALUT est stocké en mémoire.
En remarquant que 65 + 32 = 97, représentez comment le mot salut (en minuscules) est stocké en mémoire, sans refaire la conversion pour chaque lettre.
Représentez sous forme binaire l'adresse IP : 192.168.1.15, sous forme de 4 octets, en rajoutant pour chaque octet des 0 à gauche si nécessaire.

Base 16 - Système hexadécimal

Le principe est le même que pour n'importe quelle base. On a besoin de 16 symboles, et nos 10 chiffres habituels ne suffisent pas, on les complète avec les 6 premières lettres de l'alphabet.
Base 16 0 1 2 3 4 5 6 7 8 9 A B C D E F
Base 10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Utile pour la suite

160
1		161
16		162
256		163
4 096		164
65 536
1162564 09665 536
2325128 192131 072
34876812 288196 608
4641 02416 384262 144
5801 28020 480327 680
6961 53624 576393 216
71121 79228 672458 752
81282 04832 768524 288
91442 30436 864589 824
101602 56040 960655 360
111762 81645 056720 896
121923 07249 152786 432
132083 32853 248851 968
142243 58457 344917 504
152403 84061 440983 040
162564 09665 5361 048 576
160 = 1
161 = 16
162 = 256
163 = 4 096
164 = 65 536
165 = 1 048 576
166 = 16 777 216
167 = 268 435 456

Conversion base 16 → base 10

Exemple :
(1B2)16 = (1 x 162 + 11 x 161 + 2 x 160)10
= (256 + 176 + 2)10
= (434)10
163
4096		 162
256		 161
16		 160
1		 SOMME
base 10

1
1 x 256
256		 B
11 x 16
176		 2
2 x 1
2

434
Autres exemples : 
(1 A)16 = (1 x 16 + 10 x 1)10

(3 A 5)16 = (3 x 256 + 10 x 16 + 5 x 1)10

(1 0 1 1)16 = (1 x 4096 + 0 x 256 + 1 x 16 + 1 x 1)10

(1 0 1 1)2 = (1 x 8 + 0 x 4 + 1 x 2 + 1 x 1)10

(4096)10 = (162)10 = (100)16
Convertir en base 10 :
  • (15)16
  • (7)16
  • (F)16
  • (16)16
  • (ABC)16
  • (FADA)16
  • (19DD5)16
  • (28FEC)16
(1 5)16 = = "1 seizaine" + 5 unités = (1 x 16 + 5 x 1)10

(A B C)16
    = (A "256aines" + B "seizaine" + C unités)10
    = (10 x 256 + 11 x 16 + 12 x 1)10
    = (2560 + 176 + 12)10
    = (2748)10

Conversion base 10 → base 16

Fonctionne exactement comme en base 2, avec la méthode des restes et la méthode des divisions successives.

Exemple utilisant la méthode des restes : convertir le nombre (853)10 en base 16 :
On se demande : quelle est la plus grande puissance de 16 qui "tient" dans 853 ?
La réponse est 256 (162), que 853 peut contenir 3 fois.
Nous indique qu'il y a un 3 dans la case des 16 3 :
162
256		 161
16		 160
1		 SOMME
Base 10
3
3 x 256
= 768		 ?
?		 ?
?
853
On a casé 768, reste à caser 853 - 768 = 85

On recommence avec 85 : quelle est la plus grande puissance de 16 qui "tient" dans 85 ?
La réponse est 16 (161), que 853 peut contenir 5 fois.
162
256		 161
16		 160
1		 SOMME
Base 10
3
3 x 256
= 768		 5
5 x 16
= 80		 ?
?
853
On a casé 80, reste à caser 85 - 80 = 5

On recommence avec 5 : quelle est la plus grande puissance de 16 qui "tient" dans 8 ?
La réponse est 1 (160), que 5 peut contenir 5 fois.
162
256		 161
16		 160
1		 SOMME
Base 10
3
3 x 256
= 768		 5
5 x 16
= 80		 ?
5 x 1
= 5
853
Le reste vaut mainenant 0 et le processus s'arrête.

Finalement, (853)10 = (355)16
Convertir en base 16 :
  • (15)10
  • (16)10
  • (26)10
  • (100)10
  • (255)10
  • (15 945)10
  • (41 628)10

Addition en base 16

+ 0 1 2 3 4 5 6 7 8 9 A B C D E F
0 0 1 2 3 4 5 6 7 8 9 A B C D E F
1 1 2 3 4 5 6 7 8 9 A B C D E F 10
2 2 3 4 5 6 7 8 9 A B C D E F 10 11
3 3 4 5 6 7 8 9 A B C D E F 10 11 12
4 4 5 6 7 8 9 A B C D E F 10 11 12 13
5 5 6 7 8 9 A B C D E F 10 11 12 13 14
6 6 7 8 9 A B C D E F 10 11 12 13 14 15
7 7 8 9 A B C D E F 10 11 12 13 14 15 16
8 8 9 A B C D E F 10 11 12 13 14 15 16 17
9 9 A B C D E F 10 11 12 13 14 15 16 17 18
A A B C D E F 10 11 12 13 14 15 16 17 18 19
B B C D E F 10 11 12 13 14 15 16 17 18 19 1A
C C D E F 10 11 12 13 14 15 16 17 18 19 1A 1B
D D E F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C
E E F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D
F F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E
Calculer les additions suivantes en base 16 :
  • (8 + 5)16
  • (A + B)16
  • (FF + 1)16
  • (1F4 + 102)16

Multiplication en base 16

x 0 1 2 3 4 5 6 7 8 9 A B C D E F
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 1 2 3 4 5 6 7 8 9 A B C D E F
2 0 2 4 6 8 A C E 10 12 14 16 18 1A 1C 1E
3 0 3 6 9 C F 12 15 18 1B 1E 21 24 27 2A 2D
4 0 4 8 C 10 14 18 1C 20 24 28 2C 30 34 38 3C
5 0 5 A F 14 19 1E 23 28 2D 32 37 3C 41 46 4B
6 0 6 C 12 18 1E 24 2A 30 36 3C 42 48 4E 54 5A
7 0 7 E 15 1C 23 2A 31 38 3F 46 4D 54 5B 62 69
8 0 8 10 18 20 28 30 38 40 48 50 58 60 68 70 78
9 0 9 12 1B 24 2D 36 3F 48 51 5A 63 6C 75 7E 87
A 0 A 14 1E 28 32 3C 46 50 5A 64 6E 78 82 8C 96
B 0 B 16 21 2C 37 42 4D 58 63 6E 79 84 8F 9A A5
C 0 C 18 24 30 3C 48 54 60 6C 78 84 90 9C A8 B4
D 0 D 1A 27 34 41 4E 5B 68 75 82 8F 9C A9 B6 C3
E 0 E 1C 2A 38 46 54 62 70 7E 8C 9A A8 B6 C4 D2
F 0 F 1E 2D 3C 4B 5A 69 78 87 96 A5 B4 C3 D2 E1
Calculer les multiplications suivantes en base 16 :
  • (8 x 5)16
  • (A x B)16
  • (FF x FF)16
  • (1F4 x 102)16

Conversion base 16 → base 2

Le fait que 16 = 24 permet un passage facile entre ces deux bases.

Utilisations de l'hexadécimal

En programmation, la valeur d'un nombre exprimé en hexadécimal est généralement préfixée de 0x.
Par exemple : 
a = 0x12    // signifie (12)16 = (18)10
b = 12      // signifie (12)10
Recherche perso
Regardez comment les codes couleurs sont fabriqués en html. Chaque composante rouge, vert, bleu est exprimée en hexadécimal.
Exercice d'application : Couleurs javascript.
Recherche perso
Trouvez une description de la fabrication d'une IP V6 et voyez comment la base 16 est utilisée.