Exercice Calcul approché de Pi

On va utiliser diférentes formules permettant de calculer une valeur approchée de pi, que l'on pourra comparer à la valeur de la constante java.lang.Math.PI : 3.141592653589793.

Voir aussi : cet exercice sert de base à un autre exercice : Utilisation de Strategy pour calculer pi

Formule d'Euler

Leonhard Euler a démontré en 1735 (cf wikipedia) la formule :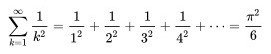 pi - formule d'Euler 1735

Autrement dit, si on appelle somme la somme (1 / 1 ²) + (1 / 2 ²) + (1 / 3 ²) + ...
on a : pi = racine carrée de (6 * somme)
ou en java : pi = Math.sqrt(6.0 * somme)

Ecrire une classe Pi1 qui contient :

Une fonction public static double calculePi(int N), où N est le nombre de termes utilisés dans la somme.
calculePi() contient l'implémentation de la formule (effectue le calcul de la somme et renvoie la valeur).
Une fonction public static void main(String[] args) qui prend en paramètre le nombre de termes à additionner.
main() appelle calculePi() et affiche le résultat.

Pour obtenir un int à partir de l'argument passé en paramètre (de type String), vous pouvez utiliser Integer.parseInt(args[0]).

Vous aurez éventuellement besoin de la fonction java.lang.Math.pow(double a, double b).

Formule de Madhava, Gregory et Leibniz

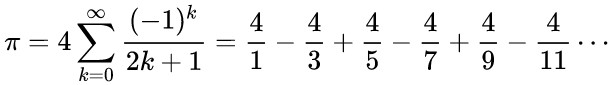
De la même manière, écrire une classe Pi2 implémentant cette formule : pi - Formule de Madhava, Gregory et Leibniz

Formule de Nilakantha

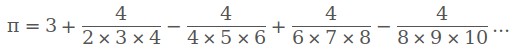
De la même manière, écrire une classe Pi3 implémentant cette formule : pi - Formule de Nilakantha

Comparaison

Quelle est la formule qui converge le plus vite ?
Pour le savoir, écrivez une classe Comparaison, avec une fonction main() qui prend toujours en paramètre le nombre d'itérations à effectuer, puis appelez successivement les fonctions calculePi() des 3 classes précédentes.
Comparez chaque résultat avec la valeur de Math.PI.

Exemple d'affichage :

java Comparaison 10000

Nombre d'itérations : 10000
Math.PI = 	3.141592653589793
pi1 = 		3.1414971543976273	 - différence = 9.549919216578218E-5
pi2 = 		3.1414926535900345	 - différence = 9.99999997586265E-5
pi3 = 		3.141592653590042	 - différence = 2.4868995751603507E-13

Notez au passage qu'on a un exemple de programme ayant plusieurs fonctions main().